قضیه ایگوروف : فرض کنیم $(X,{\cal M},\mu)$ یک فضای اندازه باشد و $E$ یک مجموعه اندازه پذیر با اندازه متناهی $\mu(E)<\infty$ باشد. دنباله $\{f_n\}$ از توابع اندازه پذیر روی $E$ که ت. ه متناهی و روی $E$ ت. ه همگرا می باشند را در نظر می گیریم. برای هر $0< \epsilon$ زیر مجموعه $A\subset E$ وجود دارد بطوریکه $\mu(E-A)<\epsilon$ و دنباله $\{f_n\}$ روی $A$ همگرای یکنواخت می باشد.

اولین سوالی که در این قضیه مطرح می شه اینه که منظور از همگرایی در صورت قضیه چی هست؟ چون همگرایی در فضای متریک برامون بدون ابهام مشخص هست:
فرض کنیم $ X$ یک فضای متریک باشد و $ \{x_n\}$ یک دنباله از عناصر $X $ باشد و می گوییم دنباله فوق همگرا به $ x$ می باشد اگر برای هر $ 0< \epsilon$، بجز تعداد متناهی عضو $x_n $ بقیه عناصر دنباله داخل گوی ${\mathbb B}(x,\epsilon) $ قرار داشته باشند.
البته این یک صورت از تعریف دنباله همگرا در فضای متریک می باشد. ولی وقتی عناصر دنباله تابع باشن چی؟؟؟

فرض کنیم $X $ یک فضای متریک باشد و دنباله $ \{f_n\}$ از توابع حقیقی با دامنه $X $ را در نظر می گیریم یعنی
\[ \forall n\in\mathbb N\quad f_n:X\to\mathbb R \] حال وقتی صحبت از همگرایی می کنیم باید محتاط باشیم چون عناصر دنباله خودشون تابع هستند و در هر نقطه از $X$ مقدار خاصی را اختیار می کنن. پس برای بررسی همگرایی دنباله ابتدا نقطه ای از $X$ مانند $x_0$ را در نظر می گیریم. لذا با قرار دادن نقطه $x_0$ در دنباله $ \{f_n\}$، دنباله $ \{f_n(x_0)\}$ از اعداد حقیقی را داریم. پس فرض کنیم $E\subset X$ زیرمجموعه ای از $X$ باشد بطوریکه برای هر $x\in E$ دنباله $\{f_n(x)\}$ دنباله ای همگرا باشد. و همچنین فرض کنیم $f_n(x)\to y_x$. حال با توجه به یکتایی حد نتیجه می شود که تابع $f(x)$ که بصورت $ f(x)=y_x$ تعریف می شود خوش تعریف می باشد. در نتیجه ما توانستیم تابعی تعریف کنیم روی $E$ بطوریکه در هر نقطه از $E$ حد دنباله $\{f_n(x)\}$ برابر $f(x)$ می باشد.
به این نوع تعریف از همگرایی، همگرایی نقطه به نقطه می گوییم. البته این نوع از همگرایی اون خواصی مطلوبی که ما انتظار داریم را برآورده نمی کنه. در زیر چن تا مثال رو بررسی می کنیم که بیشتر آشنا بشیم با مشکلاتی که این نوع تعریف همگرایی دارد:

اولین مشکل این نوع همگرایی این هست که

دنباله ای از توابع پیوسته که ممکن است بصورت نقطه به نقطه یا نقطه وار به تابعی ناپیوسته همگرا باشند

فرض کنیم $X=[0,1]$ و $f_n(x)=x^n$ آنگاه
\begin{equation*}\lim_{n\to\infty}f_n(x)=f(x)=\left\{ \begin{array}{l}0\quad\quad 0\le x< 1\\1\quad\quad x=1\end{array} \right.\end{equation*}

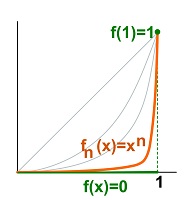
همانطور که مشاهده می شود دنباله توابع به یک تابع ناپیوسته همگرا می باشد.

مشکل دوم اینکه

مشتق دنباله همگرایی نقطه وار از توابع مشتق پذیر لزوما همگرا نمی باشد.

فرض کنیم $X=\mathbb R$ و $f_n(x)=\frac{1}{n}\sin(n^2x)$. در این حالت داریم
\[ \lim_{n\to\infty}f_n(x)=0 \] و لذا دنباله همگرای نقطه وار به $f(x)=0$ می باشد. ولی مشتق این دنباله یعنی
\[ f’_n(x)=n\cos(n^2x) \] برای هر $x$ کراندار نمی باشد. لذا برای هر $x$ همگرا نمی باشد.

و سومین مشکل

انتگرال دنباله همگرای نقطه وار از توابع ممکن است همگرا نباشد

فرض کنیم $X=[0,1]$ و $f_n(x)=\frac{2n^2x}{(1+n^2X^2)^2}$. آنگاه برای هر $x\in [0,1]$ داریم
\[ \lim_{n\to\infty}f_n(x)=0 \] ولی انتگرال $f_n$ روی $X$ برابر است با
\[ \int_0^1\frac{2n^2x }{(1+n^2x^2)^2}d x=\int_1^{1+n^2}\frac{1}{u^2}du=1-\frac{1}{1+n^2} \] و بنابراین برای هر $x\in [0,1]$ داریم
\[ \lim_{n\to\infty}\int_0^1f_n(x)dx=1 \]

لذا همگرایی از نوع نقطه به نقطه همگرایی مناسب برای تعریف همگرایی روی توابع نمی باشد!!!!

مقالات مرتبط